Create a power spectral density (PSD) plot using time series data

Dividing the results of fft() by the frequency bin width, the PSD of a time series data set can be calculated.

MakePowerSpectralDensity(sampling_frequency, data_vector)

Arguments

sampling_frequency	Numeric value specifying sampling frequency in hertz. If data is sampled once every second, then sampling frequency is 1 Hz. If data is sampled once every 2 seconds, then sampling frequency is 0.5 Hz.
data_vector	Vector of numeric values. Time series vector of data.

Value

A List with two objects:

1. Vector of frequencies in Hz. The maximum frequency should be half the sampling frequency. Called Nyquist Frequency.

2. Vector of PSD values corresponding with each frequency. Units should be in the original units of the data vector squared and divided by frequency.

The vector of frequencies can be used as the x-axis values of a single sided spectrum amplitude plot. The vector of PSD values can be used as the y-axis values of the PSD plot.

Details

If time series is a vector of accelerometer data, then the outputted y-axis will have units of (acceleration^2)/Hz.

Explanations of some of the math: https://www.mathworks.com/help/signal/ug/power-spectral-density-estimates-using-fft.html

https://blog.endaq.com/why-the-power-spectral-density-psd-is-the-gold-standard-of-vibration-analysis

https://endaq.com/pages/power-spectral-density

https://medium.com/analytics-vidhya/breaking-down-confusions-over-fast-fourier-transform-fft-1561a029b1ab

Examples

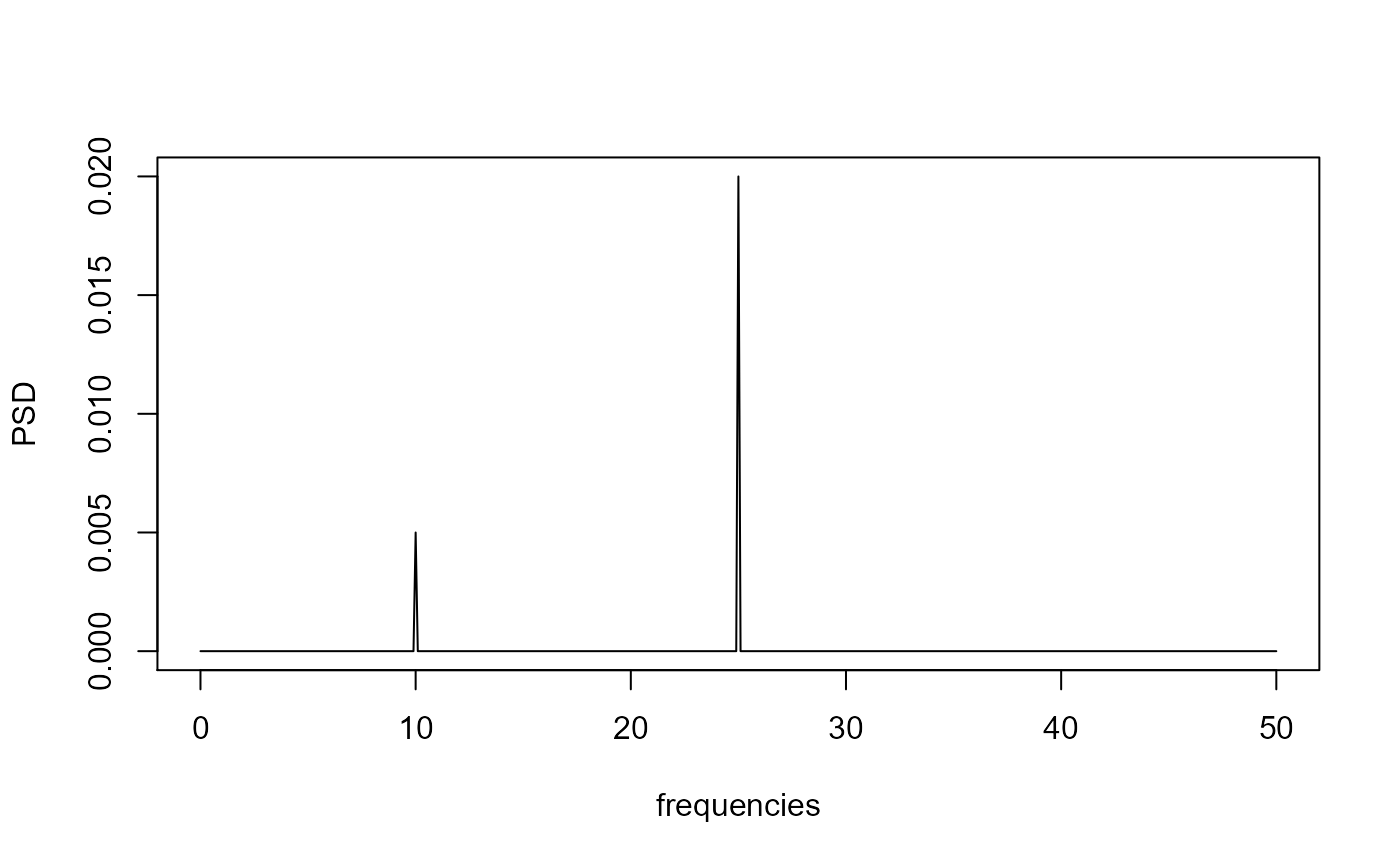
#Create a vector of time that represent times where data are sampled.
Fs = 100; #sampling frequency in Hz
T = 1/Fs; #sampling period
L = 1000; #length of time vector
t = (0:(L-1))*T; #time vector

#Form a signal (time series) that contains two frequencies:
#1. 10 Hz with amplitude of 1
#2. 25 Hz with amplitude of 2
S <- 1*sin(2*pi*10*t) + 2*sin(2*pi*25*t);

results <- MakePowerSpectralDensity(Fs, S)

frequencies <- results[[1]]

PSD <- results[[2]]

#dev.new()
plot(frequencies, PSD, type = "l")